Context

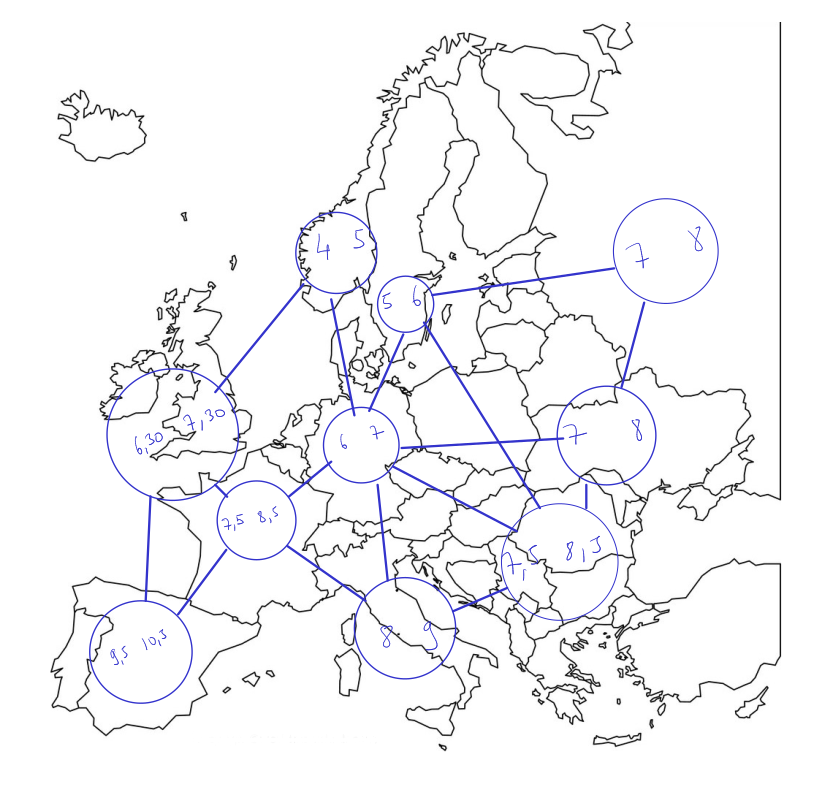
A couple days ago a friend of mine shared this map of europe and naturally came the question: How many dinners could we attend in one day ? It looked like an easy enough graph problem that is certainly NP-hard, so I decided to dive into the problem.

Problem’s statement

Let say we have a graph $G = (V, E)$ with $N$ vertices. Each vertice $v \in V$ represents a country and holds a tuple $(T_v^B, T_v^E) \in R_+$ the times at which the dinner begins and ends. The edges of our graph hold the travel time between two places, we denote for $u,v \in V, D(u,v) \in R_+ \cup \set{+\infty}$ the distance/travel time between $u$ and $v$.

The decision problem we are looking at is stated as follow: For $M$ a natural numbler, is there a simple path $ (v_1 \cdots v_K)$ such that:

• \(\forall i \in [1, K-1], \, T_{v_i}^E + D(v_i, v_{i+1}) \leq T_{v_{i+1}}^D\) ie. we arrive on time at the next dinner while having left at the end of the last one)
• K $\geq$ M

If a route does not exist it is encoded by a distance $D(u,v) = +\infty$.

NP-completeness

Problem in NP

It is easy to show that this decision problem is actually in NP. Indeed, for a given path $ (v_1 \cdots v_K) $ and $M$, we can check both conditions in linear time with respect to the size of the solution.

NP-hardness

Now the hard part. We want to show that this problem is actually as hard as any other problem in NP. To do so we will build a reduction from the Longest Path Problem which is known to be itself NP-complete (hence NP-hard). This problem is about finding the longest simple path in a given graph, you can already see how it can relate to the problem at our hands! The associated decision problem is obviously to decide wether there exists a simple path of lenght greater than $M$.

Let say we have an instance $I$ of the Longest Path Problem, we have a graph $G = (V, E)$, with $N$ vertices and $M$. Let’s build $I’$ an instance of the Max-Dinners problem.

• We keep the same vertices, so we build $V’ = V$, and for each $v \in V’$ we set $T_v^B = T_v^E = 1$, all the dinners happen instantaneously at the very same time.
• We keep the same edges so $E’ = E$ and for all $(u,v) \in V’^2$ we set $D(u,v) = 0$ if $(u,v) \in E’$ and $+\infty$ otherwise. If the edge existed in the initial graph we can travel instantaneously through it (so we don’t miss dinner !).
• And we take M’ = M

Therefore we have $I’ = (G’=(V’, E’), M’)$.

This process describes how to build an instance of Max-dinners from a generic instance of Longest path and the built instance has a linear size with respect to the size of the initial problem. Now we have to show that $I$ has a solution if and only if $I’$ has a solution.

Let’s assume that we have $(v_1 \cdots v_K)$ a solution of $I$. We then have $K \geq M$ and we can note that it’s a simple path. Moreover, we know that $\forall i, (v_i, v_{i+1}) \in E$, therefore by construction we have $\forall i, D(v_i, v_{i+1}) = 0$ and $T_{v_i}^B = T_{v_i}^E = 1 = T_{v_{i+1}}^B = T_{v_{i+1}}$. It is then easy to check that

• $ \forall i \in [1, K-1], \, T_{v_i}^E + D(v_i, v_{i+1}) \leq T_{v_{i+1}}^D $
• K $\geq M = M’$

We can conclude that $(v_1 \cdots v_K)$ is a solution of $I’$.

Conversely, we assume that $(v_1 \cdots v_K)$ is a solution of $I’$. Since $G$ and $G’$ shares vertices and edges, $v_1 \cdots v_K$ is a simple path in $G$ too, of length $K \geq M’ = M$. Therefore it’s a solution of $I$.

We can conclude that Max-dinners is at least as hard as Longest path (it’s essentially the same problem as you just saw) and since it’s in NP, it’s NP-complete.

Solution (for those who came here wanting the answer to the question)

In a first version of this article I did not bother to include a solution to the actual problem. After complaints of some friends who don’t give a shit about maths and just want to know which planes to book I wrote down the algorithm and got the solution. The whole code is available on my github. It turned out that even with the concorde we can only attend 4 dinners in one day in Europe.

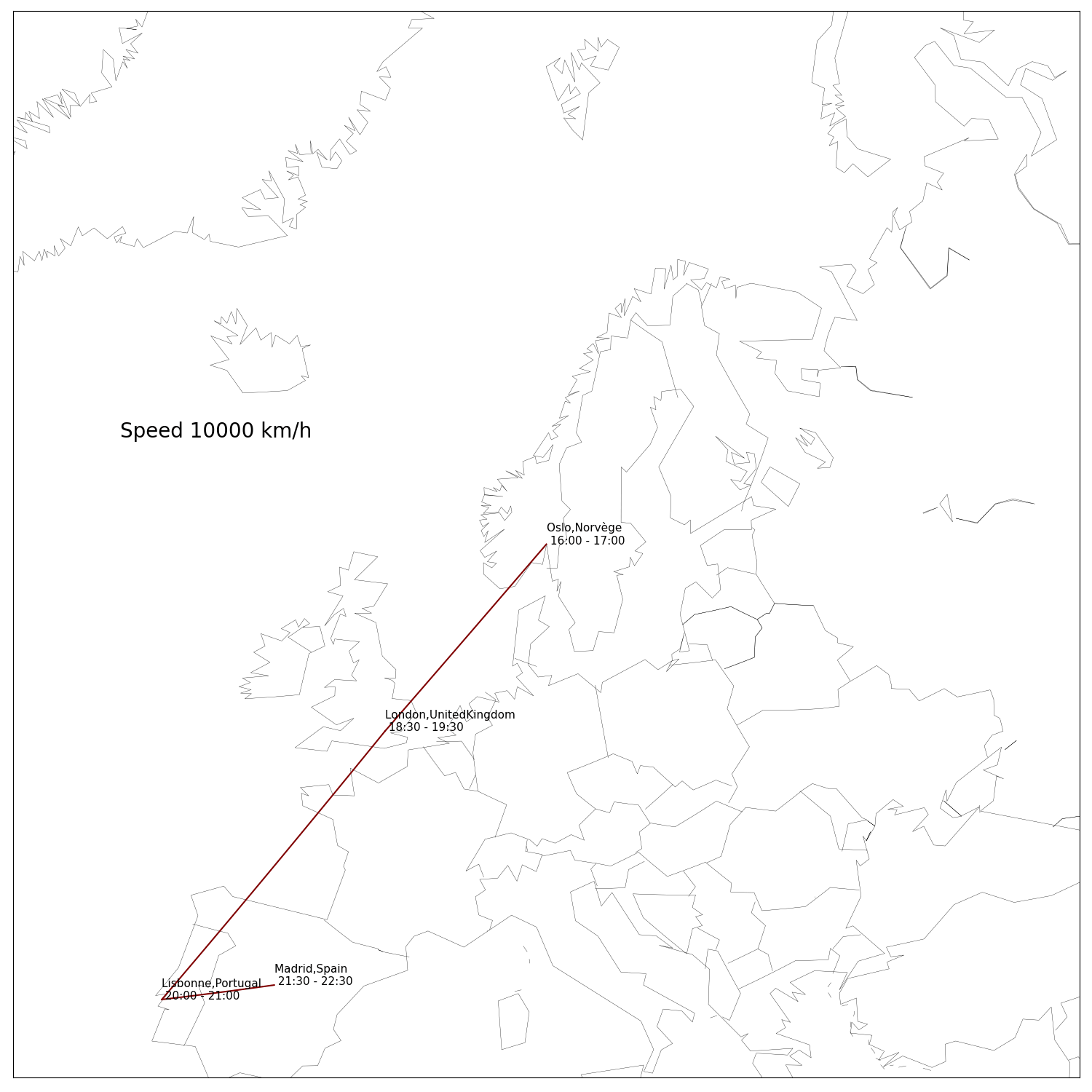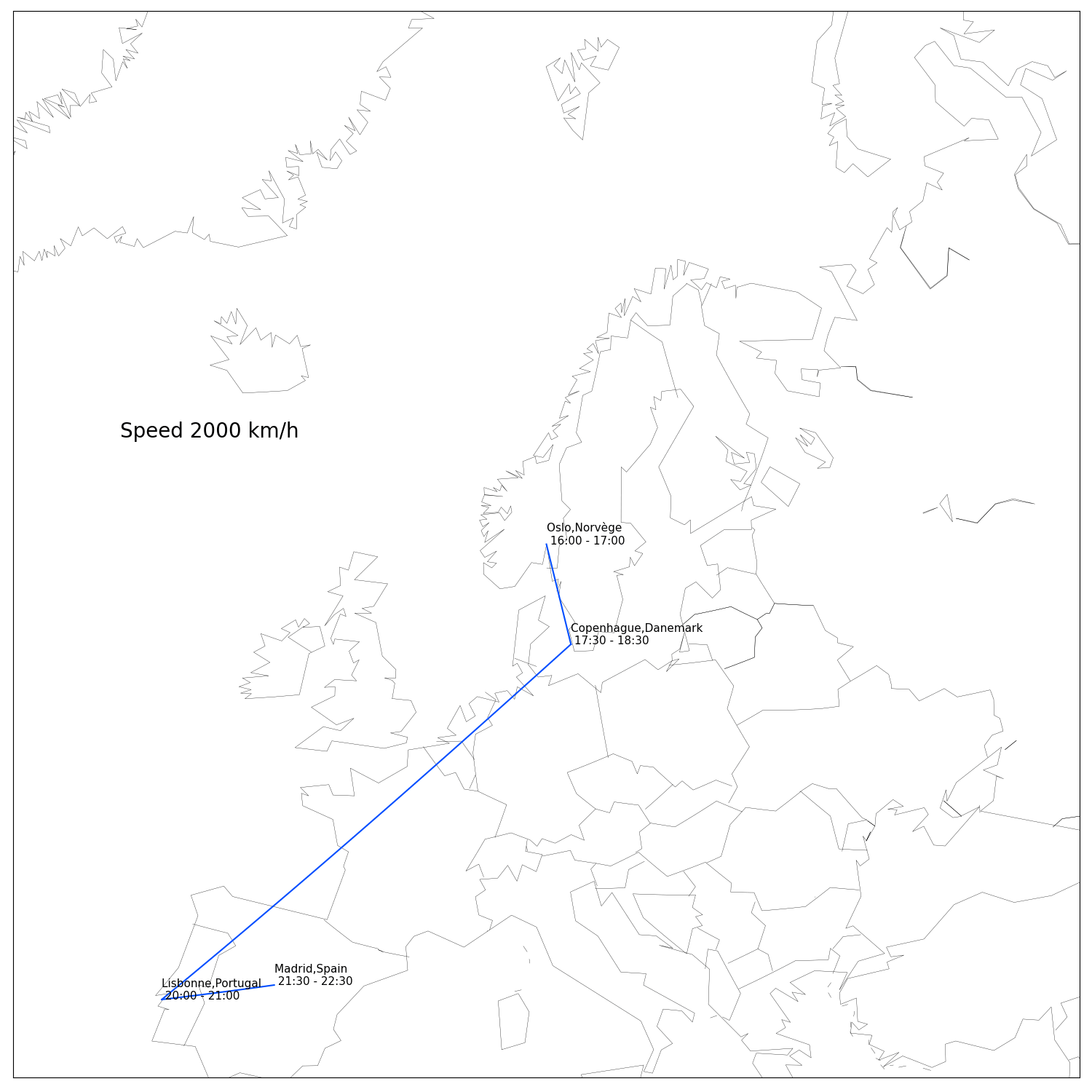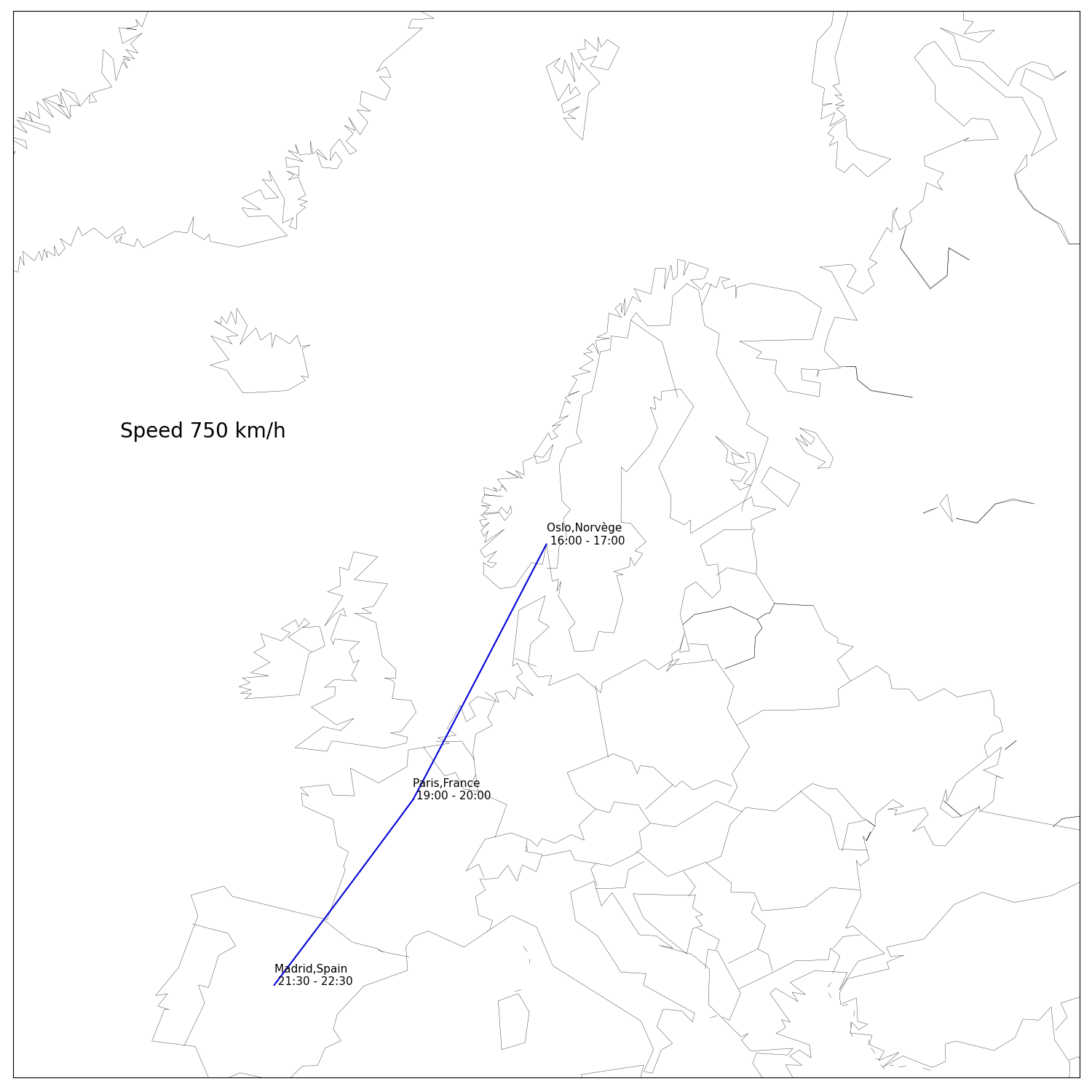
First I had to build the data:

city;dinner_b;dinner_e;lat;lon
Paris,France;19:00;20:00;48.8588897;2.3200410217200766
London,UnitedKingdom;18:30;19:30;51.5073219;-0.1276474
Madrid,Spain;21:30;22:30;40.4167047;-3.7035825
Lisbonne,Portugal;20:00;21:00;38.7077507;-9.1365919
Berlin,Germany;18:00;19:00;52.5186925;13.3996024
Oslo,Norvège;16:00;17:00;59.9133301;10.7389701
Rome,Italy;20:00;21:00;41.8933203;12.4829321
Berne,Switzerland;19:00;20:00;46.9482713;7.4514512
Kiev,Ukraine;19:00;20:00;50.4485578;30.52716228586082
Istanbul,Turkey;19:30;20:30;41.0091982;28.9662187
Stockholm,Sweden;17:00;18:00;59.3251172;18.0710935
Vienna,Austria;18:30;19:30;48.2083537;16.3725042
Warsaw,Poland;19:00;20:00;52.2319581;21.0067249
Athena,Greece;20:00;21:00;37.9839412;23.7283052
Bucarest,Romania;19:30;20:30;44.4361414;26.1027202
Copenhague,Danemark;17:30;18:30;55.6867243;12.5700724
Luxemburg,Luxemburg;18:30;19:30;49.8158683;6.1296751

And the bruteforce algorithm which comes along:

def d(t1, t2):
    return datetime.timedelta(
        hours=distance.distance((t1[3], t1[4]), (t2[3], t2[4])).km / speed
    )

def maxdinners(current_path, left):
    bpath = []
    path = []

    for i in left:
        if len(current_path) == 0:
            current_path.append(i)
            path = maxdinners(current_path, left - {i})
            current_path.pop()
        else:
            if tuples[i][1] >= tuples[current_path[-1]][2] + d(
                tuples[i], tuples[current_path[-1]]
            ):
                current_path.append(i)
                path = maxdinners(current_path, left - {i})
                current_path.pop()

        if len(path) > len(bpath):
            bpath = path

    return bpath if len(bpath) > len(current_path) else [i for i in current_path]